最小生成树,比 CSP-S 2025 T2 简单。(这个是可以说的吗)
题意
给你 \( n \times m \) 个点,\( p \) 种横向边链接每对 \( (e, a_i) \) 和 \( (e, b_i) \),\( q \) 种纵向边链接每对 \( (x_i, f) \) 和 \( (y_i, f) \),求最小生成树权值。
暴力是 \( O(nm + np + mq + (p + q) \log (p + q)) \) 的按照题意模拟跑 MST,期望 59 pts。
优化思路
考虑优化。假定存在一条横边(红色),我们将其建全后可以看为将两个纵列合并了起来(如图 1),此时当我们再尝试建纵边(绿色),对于已经合并了的列我们可以只建一条边(如图 2),此时其又会合并两个横排(如图 3)。对此我们发现每建一类边的操作相当于合并两个纵列或横排。
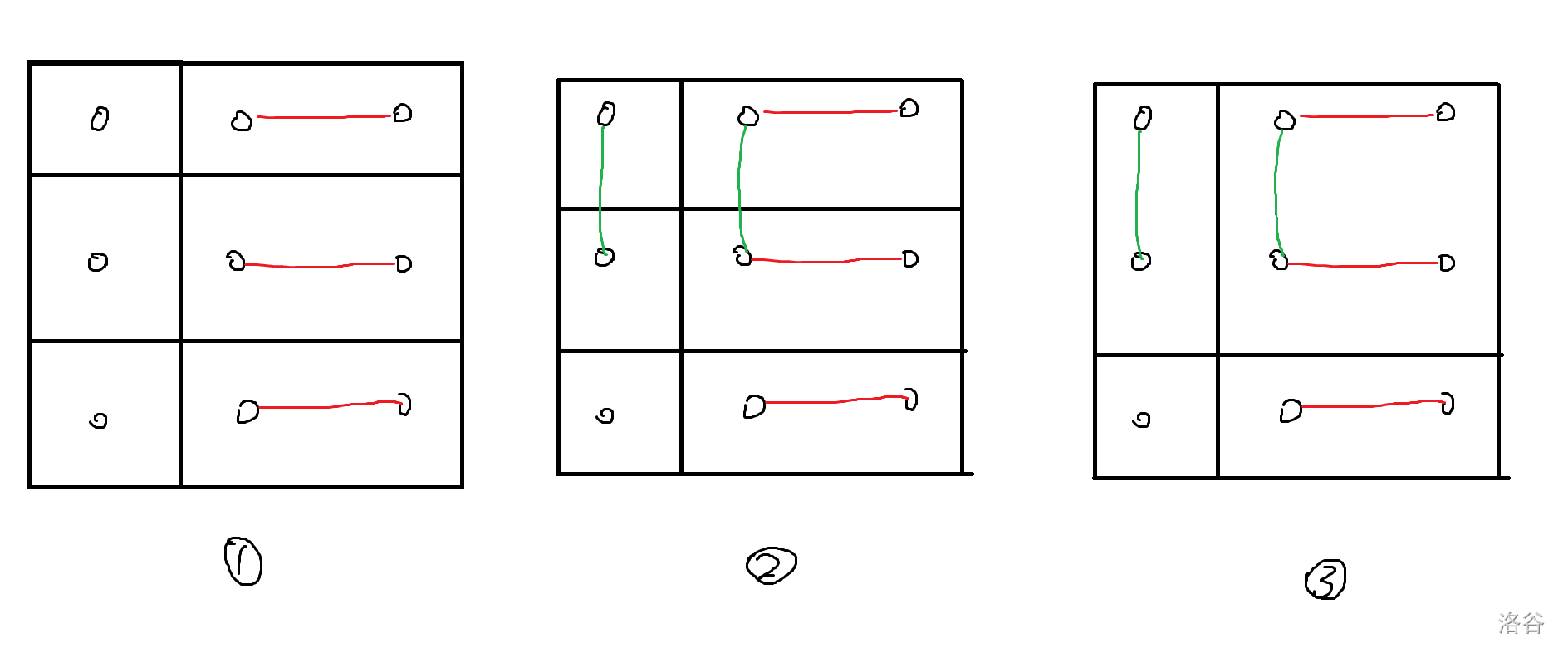
对于每一列和每一排考虑,再次假设建一条横边,所建的边数应该为合并后的排数(即横排数减去已建纵边数),纵边同理,再拿第二组样例举个例子如下(图 4):
1
2
3
4
5
6
7
8
| 2 3 4 1
-----
2 3 5
3 2 7
1 2 6
1 1 8
------
2 1 5
|
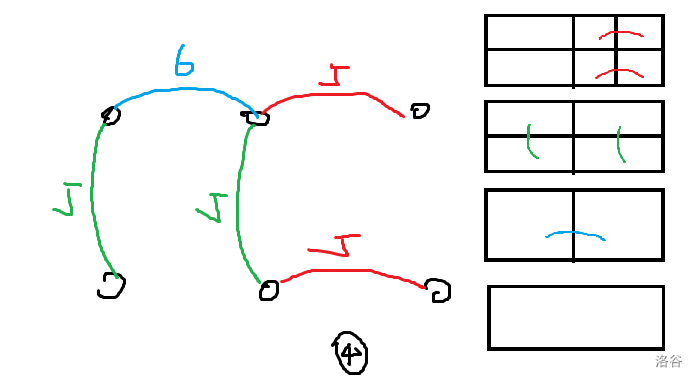
按照这个思路,对横点和纵点一起跑一边最小生成树即可。复杂度 \( O(n + m + (p + q) \log (p + q)) \)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| i64 n, m, p, q;
i64 sum;
i64 fa[N];
int Find(int u) {
if(fa[u] == u) return fa[u];
fa[u] = Find(fa[u]); return fa[u];
}
struct edge {
i64 u, v, w, fac;
bool operator < (const edge &p) const {
return w < p.w;
}
};
vector <edge> E;
void solve() {
cin >> n >> m >> p >> q;
int jud = 1;
for(int i = 1; i <= p; i++) {
i64 u, v, w; cin >> u >> v >> w;
sum += w * n, jud &= (w == 1);
E.push_back({u, v, w, 0});
}
for(int i = 1; i <= q; i++) {
i64 u, v, w; cin >> u >> v >> w;
sum += w * m, jud &= (w == 1);
E.push_back({u, v, w, 1});
}
if(jud) return cout << sum - (n * m - 1) << '\n', void();
i64 ans = 0, cntr = 0, cntc = 0;
sort(E.begin(), E.end());
for(int i = 1; i < N; i++) fa[i] = i;
for(auto [u, v, w, f] : E) {
if(!f) {
int uu = Find(u), vv = Find(v);
if(uu != vv) fa[uu] = vv, ans += (n - cntc) * w, cntr++;
} else {
int uu = Find(u + m + 1), vv = Find(v + m + 1);
if(uu != vv) fa[uu] = vv, ans += (m - cntr) * w, cntc++;
}
}
cout << sum - ans << '\n';
return void();
}
|





